難関大学現役合格への多彩な講座群
東大・京大・阪大・医学部。あなたはどの難関大学を目指しますか?希望の進路によって最適のクラスを設定しています。
選抜クラス
■受講対象中学
灘・東大寺・洛南・甲陽・大阪星光・洛星・西大和・神戸女学院・四天王寺・大教大附属各中学・奈良帝塚山・神大附属・清風南海など
英語
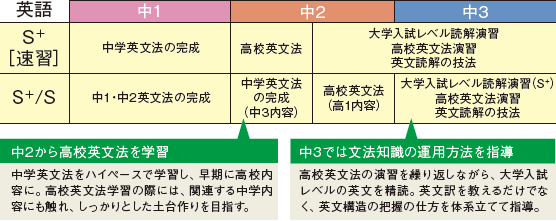
全国トップレベルの実力を養成
中1・中2時は反復練習による文法知識の定着に主眼を置き、中3からは英文解釈の力を磨いていきます
さらに、S+クラスはプラスされた時間で、学習段階に応じた発展指導を行い、中3時には難関大学入試問題に挑戦できるレベルまで英語力を引き上げます。
数学
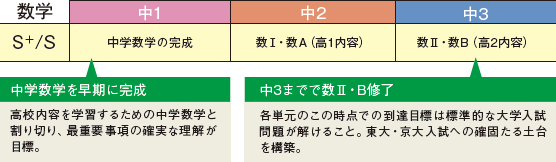
知識を習得し、思考力を養成
思考力の錬成の土台となる広く深い知識と、解答時に自由自在に使いこなせる道具を高いレベルで習得させていきます。
さらに、S+クラスはプラスされた時間で、数学力の根底部分である論理的思考力の向上に寄与する部分にも踏み込み、高校数学の各単元の学習終了時には、難関大学入学試験問題に挑戦できるレベルまで高めていきます。
Sクラス
■受講対象中学
東大寺・洛南・甲陽・大阪星光・洛星・六甲・高槻・清風・神戸女学院・四天王寺・神戸海星・金蘭千里・奈良帝塚山・奈良学園・大教大附属各中学・神大附属・京教大附属・大谷・甲南女子・明星・小林聖心・親和・京都女子・雲雀丘学など
英語
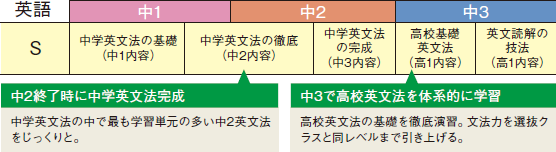
総合力を身につけるバランスのとれたカリキュラム
入試に大きく関わる文法単元を厳選し、整理して指導します。また文法を早期に確立してから反復演習するカリキュラムを組み、総合力の礎となる基礎文法を定着させ、本格的な読解に向けて無駄なく学習を進めていきます。
数学
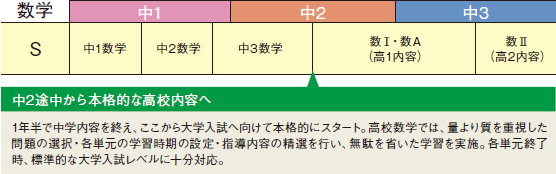
思考力と柔軟性を育てるクラス
大学入試に向けて速い進度でカリキュラムをこなすことも大切ですが、中学時代は目前のハードルを一つひとつ越えつつ、将来を見据えて思考力と柔軟性を鍛える学習こそが重要です。このことを意識し、すべてにおいて“なぜ”を考える姿勢から指導します。
学校進度対応講座

学校内容を確実にフォロー
研伸館中学生課程では、様々な学校進度対応講座を開講しています。これらの学校は、いずれも独特な進度・カリキュラムで学習しており、テストの出題形式にも特徴があります。
灘クラス
東大寺クラス
甲陽クラス
四天王寺クラス
※ここで紹介しているクラスは一部です。
各学校の授業についての対処法を経験豊富な研伸館講師から学び、研究しつくされた教材でしっかりと勉強すれば、ライバルたちに大きな差をつけることができるのです。
「学校の予習・復習を完璧にしたい」という人は、この学校進度対応講座を受講してください。
-
各学校在籍生のみを対象にしています。
学校授業の難度に応じて、講義中心・演習中心の授業を切り替え、進度調整、定期試験対策、成績管理など細かくサポートします。
-
学校の成績を上位で安定させ、大学現役合格へ。
毎年難関国公立大学に多くの合格者を出している学校では、学校の成績を上位で安定させることが後の大学現役合格につながります。そのための学習習慣の確立を重視しています。
-
3学校の授業に準拠したオリジナル教材を使用します。
基礎から応用まで様々なレベルに応じた研伸館オリジナルの教材は、学校の補習にとどまらず真の学力養成を目指し、最少の時間と労力で最大の効果を生み出します。
物理化学講座
国公立大医学部・東大・京大を目指す
理系志望の生徒にとって、理科の成績が合否の鍵を握ります。中3から4年間かけて、計画的かつ着実に知識を蓄えていきます。
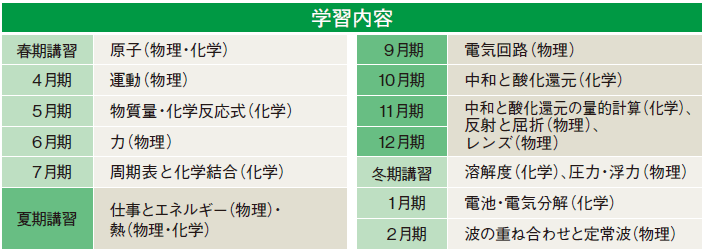
※下図の四角で囲われた内容が学習単元になります。
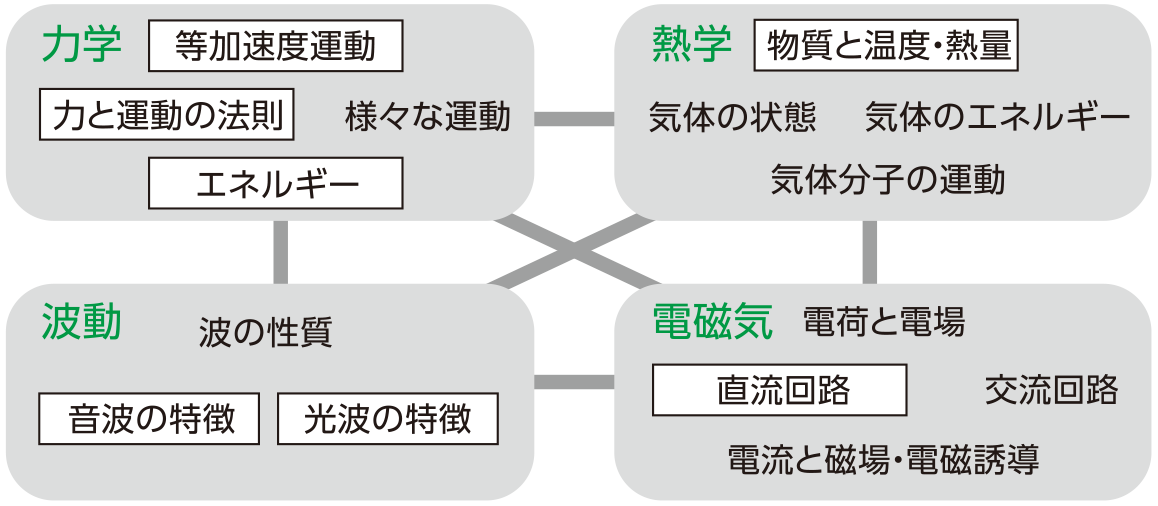
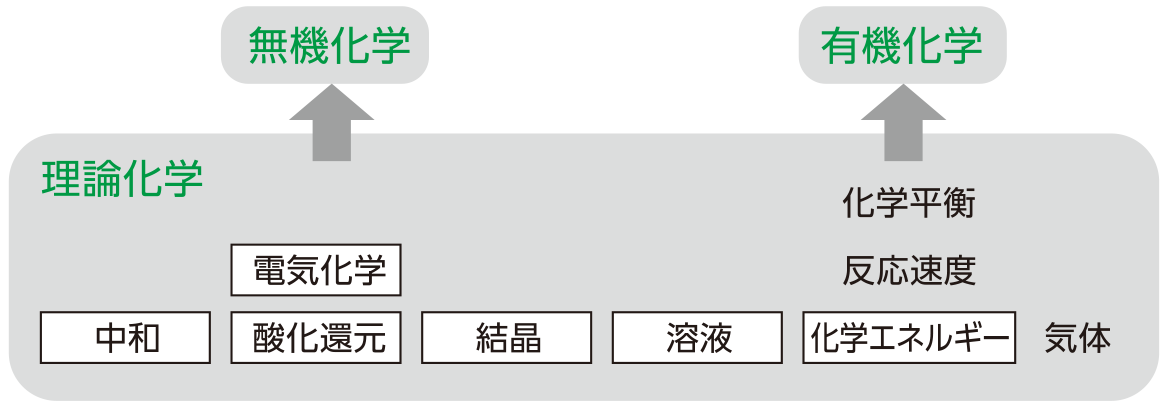
研伸館物理化学の4年一貫指導カリキュラム概念図
-
最難関大学・学部を目指した研伸館独自の4年一貫カリキュラムによる指導
-
最重要分野に的を絞った深い理論解説
-
復習テストによる確実な実力定着
国語講座

国語の力はゆっくり育まれるもの。水をやればすぐに花開くものではありません。スポーツや芸術には基礎基本の修練が大切なように、料理には下ごしらえが欠かせぬように、国語にも「言の葉」を伸ばす肥やしが必要です。受験から解き放たれた今、将来に大輪の花を咲かせるべく、一年間でじっくり言葉の基礎を学びましょう。
英語Route G(ルートグローバル)
世界基準のカリキュラムでアカデミックな英語を学べる
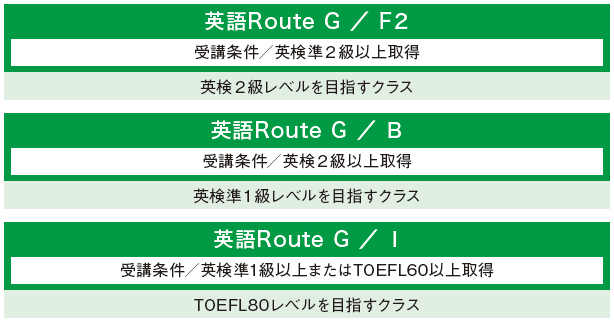
Route G(ルートグローバル)は、ベネッセが提供する、将来海外大学をも視野に入れネイティブレベルの英語力を目指す講座で、小学生時代に海外での生活経験があったり、インターナショナルスクールや英会話塾に通ったりしていて、既に英検準2級以上のレベルに至っている人が、世界基準のカリキュラムでアカデミックな英語を学べるように編成されています。
授業の一部または全てをネイティブスピーカーが担当します。RouteG/F2では高校英文法を体系的に学びながらネイティブスピーカーが担当するオールイングリッシュの授業となります。RoteG/B以上のレべルでは文法を体系的に学ぶことを目的にするクラスではありませんので、英語経験者であっても文法の体系的習得を目指す方には別の英語講座の取得もお勧めしています。
\ 将来、進路を世界中から選びたい /
そんな方のための英語講座が開講!
TOPICS
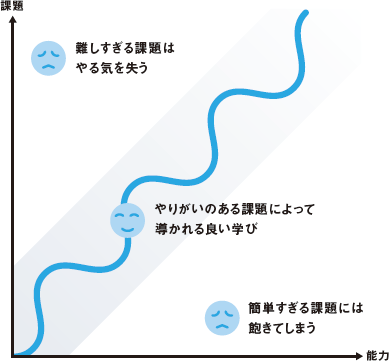
「難しすぎず、易しすぎない」クラスで勉強してもらいます!
研伸館中学生課程では、各学校の学習進度や内容を長年にわたって研究し、さらに、各校舎・各講座・各教科・各クラスの一人ひとりの状況を見て、その時々に常に最適な課題を提示し続け、「もっと知りたい」「もっと問題を解きたい」という意欲をかきたてていきます。進度やレベルに応じた独自のクラス設定も行っていますので、能力が開花し、より深く、より難しい問題を解決する意欲や学力が生まれた時期に、上位クラスへの進級という飛躍のチャンスも訪れます。
中学生時代に知見を深め、広めることで、大学入試への伸びしろが大きくなると言えるのです。

 資料請求
資料請求
 体験授業
体験授業





